Preview
动态规划方法是一种对具有交叠子问题的问题进行求解的技术。如果不同的子问题拥有公共的子子问题,那么分治算法的递归里有可能会反复地求解一个公共的子子问题。不得不承认,DP(dynamic program)大概是本书唯一能够抗衡分治法的存在了。尽管这本书没有提到Warshall和Ford,没有背包问题也没有小机器人,剩下的文字依然皓如繁星。愿天堂没有DP。
先修知识:
钢条切割问题指的是,将一条长钢条切割成几条短钢条出售,求解售价最大化问题。其中不同长度的钢条的价格不同,甚至也会出现根本不切割而利益最大的情形。也可以概括为,利用手上限额的资源,合理分配以达到利益最大化的问题。
最长公共子序列问题指的是,求解两个序列的最长的相同子序列。子序列所含元素在序列中的位置下标应该是严格递增的。例如,Z={B,C,D,B}是X={A,B,C,B,D,A,B}的子序列,此时位置下标为{1,2,4,6}。
钢条切割
我们来研究一下钢条切割问题。
| 长度i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 价格p | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 30 |
如果要考虑总价最高的算法,直接求单位价格是不合理的。我们先利用穷举的方法考虑总长n=4英寸时的情况:
4 1 3 2 2 3 1
1 1 2 1 2 1 2 1 1 1 1 1 1
4英寸钢条的8种切割方案
当长度为4英寸的钢条被切割成两条2英寸的钢条时,总价格最高为10,为最优解。同时我们也发现,单位价格最高的长度3(8/3=2.67)并没有被选择,许多重复的情况也被考虑。我们对总长度在1~10之间的钢条全部切割一遍,并观测它们的最优切割方案:
| 总长度 | 是否产生切割 | 切割方案 |
|---|---|---|
| 1 | no | 1 |
| 2 | no | 2 |
| 3 | no | 3 |
| 4 | yes | 2+2 |
| 5 | yes | 2+3 |
| 6 | no | 6 |
| 7 | yes | 1+6 or 2+2+3 |
| 8 | yes | 2+6 |
| 9 | yes | 3+6 |
| 10 | no | 10 |
我们可以发现这么几点规律(至少对于1~10的长度而言):
-
如果单价高于所有小于自己长度的单价,则不切割,并作为一个最优子结构
-
如果单价低于任意一个小于自己长度的单价,则切割为数个最优子结构
-
由于「总长度为1」本身一定是最优子结构,因此任何一种长度都可以分割成最优子结构。
显然地,钢条的切割只能是最优解。它要么自成一派,成为一个最优子结构,要么一定是几个最优子结构的和——除非它无法被分解为几个最优子结构,然而这对于钢条切割来说是不可能的,「总长度为1」本身一定是最优子结构。
证明「切割为数个最优子结构」的操作的正确性可以利用数学归纳法,在此不表。每一次都利用上一个或者上一些子问题的最优解来计算这一个子问题的最优解,看上去就像依次递归一样。因此,我们把这个规律推广开来,并实现钢条切割问题的递归通解:
CUT(p,n)//p is an array of price
if n == 0//finish cut
return 0
q = 0
for i =1 to n
q = max(q, p[i] + CUT(p, n-i))
return q
如果画出这个算法的递归树,会发现这个算法难以处理大规模的数据—— 每次调用cut(p, n-i)都会把已经计算过的情形再次调用一遍。 实际上这个算法的时间复杂度为2^n级别。这是递归方法的一个巨大缺陷,直接从顶向下的递归实现需要一个数据记录。
为了改进这个算法,我们有两种方式——其一是对从顶向下的实现加上一个数据记录,其二是干脆用自底向上来实现。前者虽然时间复杂度差不多但分析比较麻烦,我们用自底向上会方便不少。
BOTTOM-UP-CUT(p, n)
r[0...n] be a new array
r[0] = 0
for j = 1 to n
q = 0//用q来储存最优子结构
for i = 1 to j
q = max(q, p[i] + r[j-i])
r[j] = q
return r[n]
在这个过程中,我们引入了动态规划的思想,也就是仔细安排求解的顺序,以达到每个子问题只求解一次的极高效率,同时将结果保存下来。因此用时Θ(n^2)。
值得注意的是,如果我们要给出真正的答案,还需要重构解,让每个最优子结构储存相应的切割方案,最后让算法返回切割方案才能解决实际问题。

不要忘记动态规划也常常用来求解斐波那契数
动态规划原理
最优子结构
关于最优结构,我们应该有如下共识:
- 问题的一个解应该视为一种选择,我们只关心如何做出最优的选择。
- 在做出一个最优选择后,要确定哪些子问题「发生」了,「新的子问题」应当包含「旧的子问题」。
- 当前子问题本身的所有子问题必须是最优解的情形。
实际上,如果一个问题不具有最优子结构,那么它一定不适于用动态规划来求解。动态规划的本质,就是从最小的最优子结构,一步步往上扩容来达到总是最优的过程。我们的关键在于,这个问题的最优子结构的形式是什么?怎样有效选取大于当前子问题的父问题?
对于「求无权重图的两点间最短路径」这个问题而言,p→w的结构就可以被分为p→q←w的形式。确定哪个点或者说哪条临时的链作为q,然后从两边向中间不断求最优解,就能很容易地得到答案。但是对于「求无权重图最长的两点间的简单路径」却不应该用动态规划。因为p→q的最优解,有可能会与q←w的最优解存在重复路径(这与题目要求不符)。这种情形下,子问题之间互相影响了,p→q与q←w如果不存在交集的话,有可能会出现其中一个不是最优解的情况,这与我们的共识相违背。当然,求最短路径就不会出现互相影响的情况,它们的子问题是互相独立的。
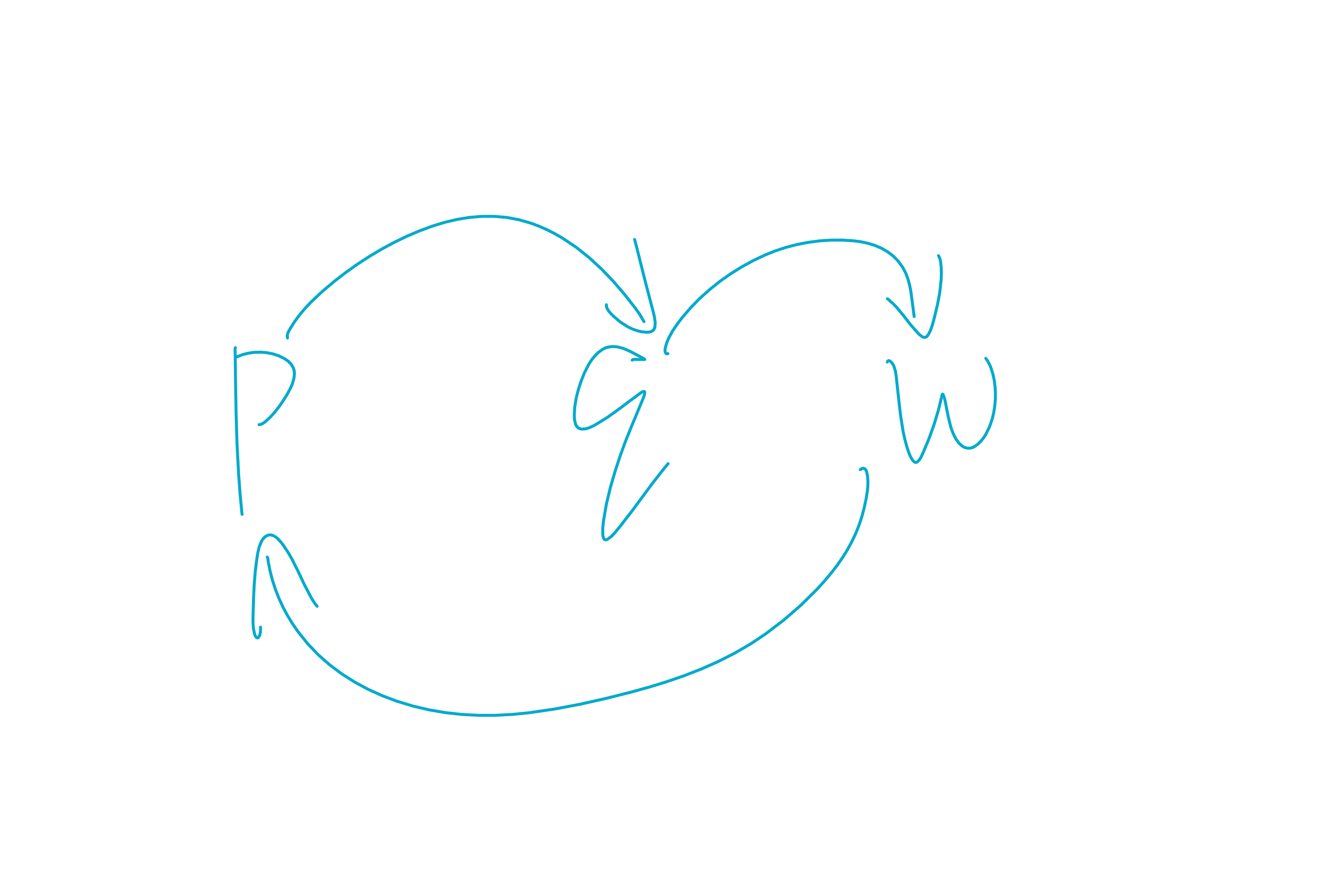
p→q与w→p→q重复路径了
重叠子问题
当一个递归算法不断调用同一问题的时候,我们说该问题包含重叠子问题。相反地,递归算法往往会在递归的时候产生全新的子问题,比如每次归并排序在递归树上前进的时候产生的排序数据都完全不一样(尤其指每个数据中的相对位置发生变化)。而动态规划则充分利用重叠子问题,每次只需要花O(1)的时间从备忘录中调用所需要的上一个子问题的数据。
动态规划需要经常重新构造一个最优解,并实时更新备忘录。如果一个问题总是产生无法用旧子问题的解来快速解答的新子问题,那么显然递归算法是更好的;而如果一个问题总是产生大量重叠子问题,那么动态规划则是更好的。递归往往自顶向下,精确细分,而动态规划往往从底往上,见微知著。
最长公共子序列
LCS可以说是曾经的噩梦了……不过它确实是动态规划一个相当有用的案例。这里我只讲到递归式。
子序列的定义是,一个序列X = <x~1~, x~2~, …, x~m~>,存在另一个序列Z = <z~1~, z~2~, …, z~n~>,其中Z序列中所有的元素都在x中存在一一对应,并且相应的元素在x中的所在位置严格递增,那么Z就是X的一个子序列。例如,Z = <B, C, D, B> 就是X = <A, B, C, B, D, A, B> 的一个子序列,相应的下标序列为<2, 3, 5, 7>。
当且仅当Z序列同时是X序列和Y序列的子序列时,Z序列是它们的公共子序列。X序列和Y序列的公共子序列中最长的为最长公共子序列。这是LCS的定义。LCS也可以看作是两组同类数据的「相似率」,LCS越长,两组数据的「共同语言」就越多。
根据我们的LCS定义,对于序列{X~1~, …, X~m~}和序列{Y~1~, …, Y~n~}的一个LCS序列{Z~1~, …, Z~k~}的子序列{Z~1~, …, Z~k-1~}应该有如下评判:
- 如果X~m~ = Y~n~,那么X~m~ = Y~n~ = Z~k~, 并且Z~k-1~是X~m-1~和Y~n-1~的一个LCS
- 如果X~m~ ≠ Y~n~,且Z~k~ ≠ X~m~,那么Z~k-1~是X~m-1~和Y~n~的一个LCS
- 如果X~m~ ≠ Y~n~,且Z~k~ ≠ Y~n~, 那么Z~k-1~是X~m~和Y~n-1~的一个LCS
我们利用这三个评判,从后向前,来确认两个序列的LCS。
LCS问题的最优子结构的递归式
LCS图示