Preview
先修知识:
一棵树不存在回路。其中除了根结点以外所有的结点都有父结点(或者说父结点为NIL),除了叶子以外所有的结点都有子结点(或者说子结点为NIL)。二叉树描述的是包含叶子和根在内的所有结点,都最多只有两个子结点(或者子树)的树结构。二叉树体系内最重要的一种叫做二叉搜索树(又叫二叉查找树),再往下分,二叉搜索树又包括平衡二叉查找树(AVL树)和红黑树等等。
扩张数据结构一般要走下列四个步骤:
- 选择一种基础数据结构
- 确定基础数据结构中要维护的附加信息
- 检验基础数据结构上的基本修改操作能否维护附加信息
- 设计一些新操作
举个例子,选取一个完全二叉树。我要维护的是结点的关键字逐层往上递减这个性质,因此修改内部代码之后,再设计一个新操作EXTRACT-MIN,就能把这个完全二叉树扩张成为一个最小堆了。
二叉搜索树
可以假定一棵二叉搜索树中的所有结点必然拥有下列属性:left, right, p ——它们分别指向结点的左孩子(left child)、右孩子(right child)和父结点(parent)。对于根结点和叶子而言,父结点/子结点指向NIL。另外,二叉搜索树还有这样的性质: node.left.key <= node.key <= node.right.key 这里的left和right指左右子树中所有的结点。
遍历
既然是一颗用来查找的树,那就必须要遍历了。二叉树中有三种常见的遍历:中序遍历(inorder)、前序遍历(preorder)和后序遍历(postorder)
遍历具体方式不再赘述,直接给个图:

考虑到二叉搜索树的性质,想把树中的关键字从小到大遍历出来,就肯定要用中序遍历了。
INORDER-TREE-WALK(x)//中序遍历的伪代码
if (x != NIL){
INORDER-TREE-WALK(x.left)
print x.key
INORDER-TREE-WALK(x.right)
}
我们假设处理一颗空的结点(只有一个结点NIL)需要一个非常小的常数时间c,而print一个结点的关键字需要常数时间d。显然地,一颗结点数为n的非空二叉树,应该有一个根节点和⌈n/2⌉个叶结点,其中根节点的父结点指向NIL,叶结点的两个子结点也指向NIL,所以这个非空二叉树要处理(n+1)个空结点。遇到空结点耗费c而遇到非空结点耗费d,因此我们得到中序遍历的T(n)上界: T(n) <= c*(n+1) + dn,也就是说,调用中序遍历需要Θ(n)时间。
查询
如果我们想查询一个元素,就没有必要先遍历再查询了。利用被查询元素的关键字的大小比较,可以很快地在二叉搜索树中找到位置。
TREE-SEARCH(x, k)//x是当前结点,k是被查询元素的关键字
if(x == NIL || k == x.key)//如果查到了尽头或者查到了正确解
return x
if(k < x.key)
return TREE-SEARCH(x.left, k)//姑且也算递归吧……
else
return TREE-SEARCH(x.right, k)
查询时间为O(h),其中h是这棵树的高度。我们之前在堆排序中就提到过,如果是堆这样的结构的话,树高应该就是logn;然而树的形状可以很多变所以只能说查询时间为Ω(logn), O(n)。
当然,这个伪代码也可以写成迭代的形式——
ITERATIVE-TREE-SEARCH(x, k)
while(x != NIL && k != x.key){
if (k < x.key)
x = x.left
else
x = x.right
}
return x
如果要查询最大或最小的结点,往右或者往左一直迭代就是了。如果要查询一个结点的前驱和后继,就需要分情况讨论(以查询后继为例子):
-
存在右子树,则迭代查询右子树的最小结点
-
不存在右子树,且这个结点是父结点的左子结点,则返回父结点
-
不存在右子树,且这个结点是父结点的右子节点,则需要用到循环:
y = x.p while(y != NIL && x == y.right) x = y y = y.p return y
还是上个图吧。

当然,如果树内存在相同的关键字,我们依然用上面的讨论来定义一个结点的前驱和后继。
插入和删除
插入和删除的重点在于如何维持二叉搜索树的性质的成立。先来看插入。
TREE-INSERT(T, z)//对树T插入一个结点z
y = NIL
x = T.root//x为结点z的暂时插入目标
while(x != NIL){
y = x//y一直跟随x
if(z.key < x.key)
x = x.left
else
x = x.right
}
//此时x应该为某个叶子的一个空子结点
z.p = y
if(y == NIL)//也就意味着树T为空
T.root = z
else if(z.key < y.key)
y.left = z
else
y.right = z
插入的关键在于使用双指针沿树下移,指针x记录了向下移动的简单路径,而指针y作为遍历指针始终保持指向x的父结点。插入的运行时间上界为O(h)。
再来看删除。删除一个结点z分为以下三种情况:
-
如果z没有子结点(或者说都是空子结点),那么就只用把它扔掉,并用NIL替代它父结点的子结点。
-
如果z只有一个子结点,那么扔掉z以后将这个子结点提到原本z的位置上,并修改相应父结点的子结点指针。
-
如果z有两个子结点(这是最麻烦的一种情况),那么先找z的后继结点x(从上面关于后继的分类讨论中我们知道肯定在z的右子树中),然后拿x替换掉z,扔掉z,再连接x与z的那两个原来的子结点;同时,对于x离去留下的空位,视作一个新的删除,并接着讨论这三种情况。
代码略了。因为删除最麻烦的情况无非是第三种一直持续从根到叶子,所以运行时间的上界仍然为O(h)。
随机构建二叉搜索树的部分就不说了,用处不大。
AVL树
书上没讲AVL,这里按学校的课件来扯一下。
AVL是一种高度平衡的二叉搜索树。除了要求本身是二叉搜索树以外,还要求每个结点的左右子树的高度之差的绝对值(平衡因子)最多为1。
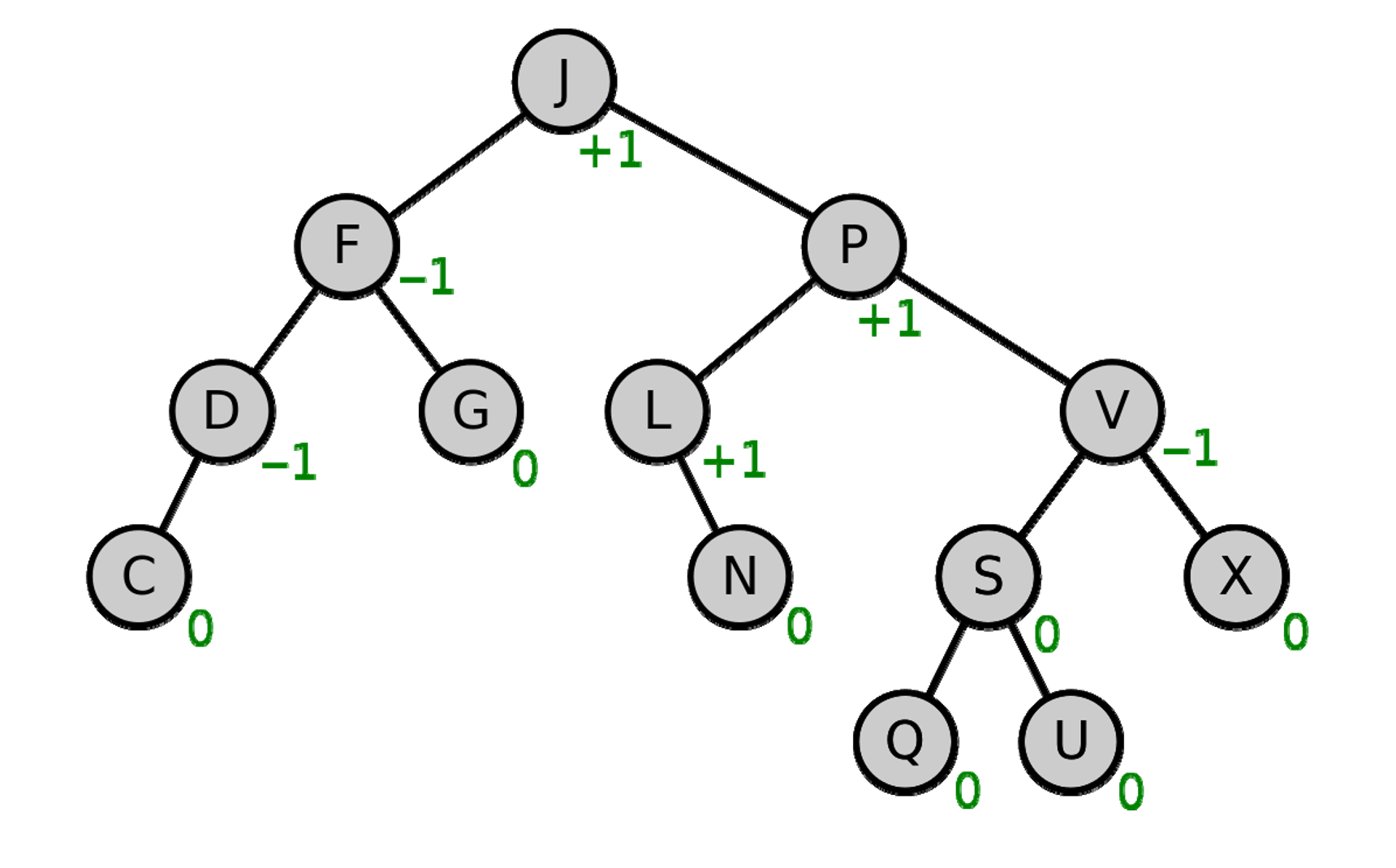
AVL树图示(带平衡因子)
这里就讲一下AVL是怎么维护自身平衡的。一般而言,只需要将AVL视作一般的二叉搜索树就行了,只是当平衡因子大于1的时候我们需要对树进行旋转(rotation)。
我们只讨论插入的时候造成平衡因子大于1的情况。显然,在插入前,AVL树的平衡因子必然刚好为1,并且这只有两种情况:左树更高,右树更高;插入一个更高的树,也无非只有两种情况:插入左子节点,插入右子节点。因此,一共有2x2=4种情况需要考虑,也就是所谓的
left-left case; left-right case; right-left case; right-right case

图片来源 GeeksforGeeks
至于删除,其实也可以套用这四种模型一一考虑。当然,插入删除遍历等等操作对于AVL树而言依然等同于二叉搜索树,只是每次操作完后需要判断是否平衡。
红黑树
红黑树也许并没有想象中的困难……如果不看具体的插入、删除等操作的话。不过这些操作正常情况下哪儿又用得到呢。
红黑树的本质也是一颗二叉搜索树。它不如AVL那样高度平衡,但是却是「近似平衡」的。其中每一个结点都有一个储存位来保存结点的颜色。有如下规则:
-
每个结点是红色或者黑色的。
-
根结点必须是黑色的。
-
叶结点必须是黑色的。
-
红色结点的两个子结点必须是黑色的。
-
一个结点到所有它的叶结点的路径上,黑色结点的数量都相同。这对所有非叶结点都有效。
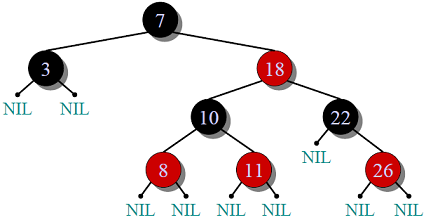
图片来源 GeeksforGeeks
这里不会对红黑树的旋转、插入等操作具体分析,只需要知道红黑树的一大性质——一颗有n个内部结点的红黑树的高度至多为2log(n+1)——就行了。(人太懒了ORZ , 整个红黑树的java实现要800行左右的代码啊,太难了)
题目答案
第十二章
12.1-2
虽然本质都是树,但是二叉搜索树是 node.left < node < node.right , 而最小堆是 node < node.left < node.right && node.thisLevel < node.nextLevel,是不能用前序遍历的。这也就意味着,堆结构只能用「维护堆的性质」的堆排序来打印有序结点。因此,耗时O(nlogn),也就是n个结点乘以每次维护堆的logn用时是堆排序必须面对的事实。
12.2-3
/*
类似于上面的检查一个结点的后继,也是分为三种情况,
有左子树,没有左子树且是父结点的右子节点,
没有左子树且是父结点的左子结点(这个最复杂)
*/
TREE-PREDECESSOR(x)
if(x.left != NIL)
return TREE-MAXIMUM(x.left)
y = x.p
while(y != NIL && x == y.left)
x = y
y = y.p
return y
12.2-7
重点肯定是查询后继结点所耗费的时间。看上面的查询后继结点的图。可以很容易知道,一条到叶节点的简单路径必然只会被遍历两次。
另外有欧拉定理r=e-v+2,因为这是平面图所以r=1,因此n个结点的树有n-1条简单路径,所以查询后继结点中的第一、三种情况加起来应该是2(n-1)次访问结点,而第二次情况每次访问1次结点。无论查询后继结点发生了多少次第一、二、三种情况,迭代加起来肯定是Θ(n)。
第十三、十四章节没有。