Preview
忙完实习后,终于有时间更新了……这一讲会讨论一些基本的数据结构和散列表。比起算法而言,数据结构应该更通用也更实用些,毕竟小项目可以只招一些API战士,而增删改查 (CRUD boy) 是绝对离不开数据结构的。书上的诸如「指针和对象的实现」就跳过了,我只用 java 和 python 。
keywords: 基本数据结构 散列技术(函数)
栈和队列
通俗地讲,栈实现了后进先出(last-in, first-out, i.e. LIFO),而队列实现了先进先出(first-in, first-out, i.e. FIFO)。利用静态数组来实现这两种结构的方式和利用动态数组的方式稍稍不一样。

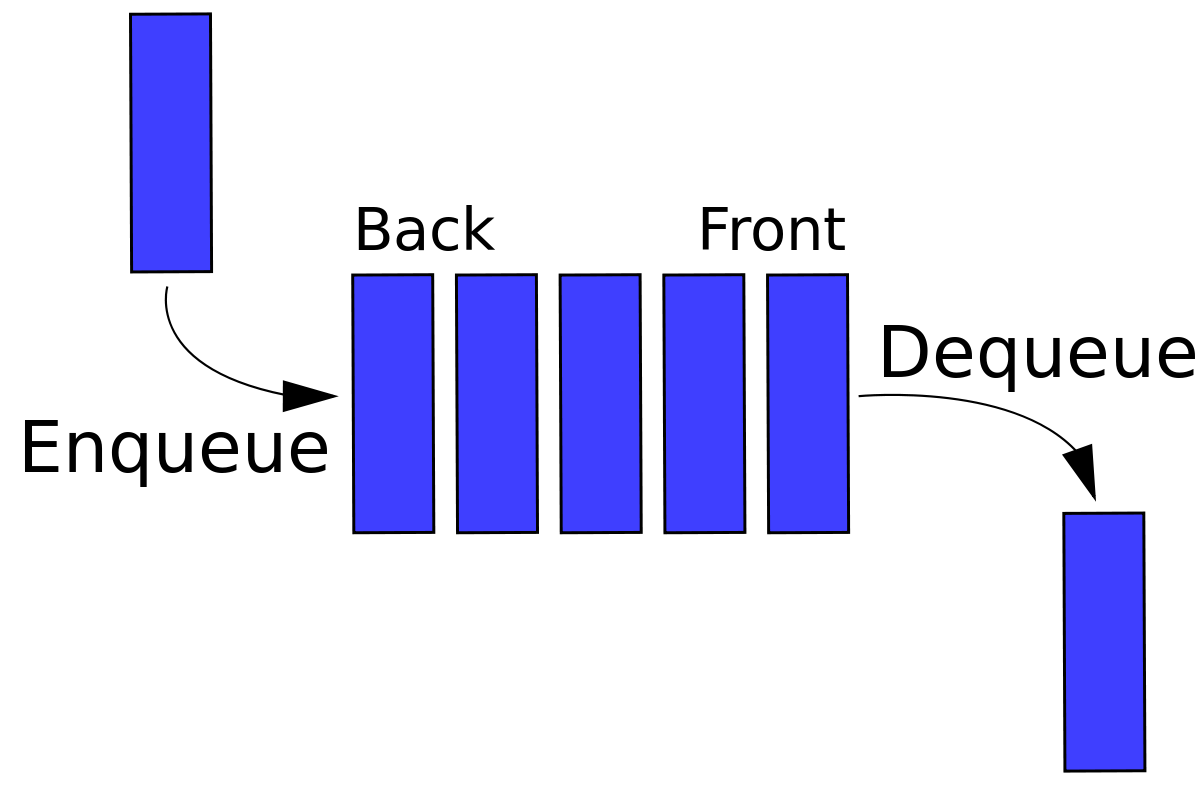
栈可以类比「羽毛球筒」,而队列可以类比「排队」,它们都可以有增删改查等操作。
关于栈
我们可以声明一个数组 array[1…n] 来储存栈,这个栈占据着数组的 array[1] 到 array[S.top]部分(其中S.top指向最新插入的元素的下标)。当我们在push的时候,我们实际在改写array[S.top+1]的值并把S.top+=1;当我们在pop的时候,我们实际在把S.top-=1并返回 array[S.top+1]。 因此,栈和实现它的数组其实只是相关联的关系,并且我们通过改变S.top来指定数组中的部分元素为栈。
STACK_EMPTY(array)
if S.top == 1
return true
else return false
PUSH(array, x)
S.top++
array[S.top] = x
POP(array)
if STACK_EMPTY(array)
error "underflow"
else S.top--
return array[S.top+1]
对于空的栈,pop操作会导致栈下溢;对于S.top已经达到n的栈,push操作会导致栈上溢(i.e. stack overflow)。
关于队列
我们依然可以声明一个数组array[1…n]来储存队列,这个队列不如栈那么耿直,它的Q.head甚至有可能在Q.tail的后面。总的来说更像一个环序,位置1在位置n后面紧紧跟随。当然,我们只需要关注队首和队尾(其中队首Q.head指向队列的最旧的元素,队尾Q.tail指向队列的最新的元素的下一个位置)。当我们在enqueue的时候,我们实际在改写array[Q.tail]的值并把Q.tail+=1;当我们在dequeue的时候,我们实际在把Q.head+=1并返回 array[Q.head-1]。
ENQUEUE(array, x)
array[Q.tail] = x
if Q.tail == array.length
Q.tail = 1
else
Q.tail++
DEQUEUE(array)
x = array[Q.head]
if Q.head = Q.length
Q.head = 1
else Q.head++
return x
对于Q.head=Q.tail的情况,队列为空,此时如果试图删除队列中的一个元素,则队列发生下溢(underflow)。对于Q.head=Q.tail+1的情况,队列为满(有一个空间不用),此时如果试图增加一个元素进队列,则队列发生上溢(overflow)。
上面那个伪代码没考虑上溢和下溢。
链表
现在来谈谈链表。数组的线性顺序由下标决定,因此各类操作(CRUD)都很简单,但是链表的线性顺序由对象内部的指针决定,因此操作有点点变化。
链表可以有序,也可以无序;可以单链,也可以双链;甚至还有循环链表,不过我们统统都不管,现在只讨论无序双向链表。
双向链表中,设有元素x,那么x.prev指向前驱,而x.next指向后继,x.prev=NIL(大概是空指针的一种?)则元素x是链表L的head,x.next=NIL则元素x是链表L的tail,L.head=NIL则链表L为空。
链表的搜索
LIST-SEARCH(L,k)
x = L.head
while (x != NIL && x != k)
x = x.next
return x
链表的搜索只能采取线性方法。如果链表是有序的,那么可以二分链表来查找(这里不展开)。
链表的插入
LIST-INSERT(L, x)
x.next = L.head//把x的后继节点设为L.head
if L.head != NIL
L.head.prev = x
L.head = x
x.prev = NIL//把x的前驱节点设为NIL
这是往链表的最前头插入一个元素,运行时间是O(1)。如果要将元素插入指定地点,则先搜索到指定地点,设定插入元素的prev和next,再删除前后节点之间的关系(如果插入的地方不是最前面或者最后面的话)。
链表的删除
LIST-DELETE(L, x)
if x.prev != NIL
x.prev.next = x.next
else L.head = x.next//如果x是链表头则把下一个元素设成链表头
if x.next != NIL
x.next.prev = x.prev
注意,这里的删除和上面插入中的删除不同,想要实现还需要先遍历,然后再删除第一个找到的元素。只删除的部分运行时间为O(1),而遍历则需要Θ(n)。
上述三种操作都需要对边界条件进行操作。我们可以假设链表有一个代表空指针的对象L.nil,那么它是这样的一个对象,后继同时指向表头和表尾,同时又是表头和表尾的后继。即,L.nil.next指向表头,L.nil.head指向表尾 。另外地,有了这样的操作后我们就不再需要 L.head 和 L.tail 这两个属性了。
当然,对于一个空的链表,L.nil的前驱和后继都指向自己。代码实现简单就不一一写了。不要过分使用L.nil以造成空间浪费。 (其实除了赋空指针以外,还有利用异或构建双链表,来达到逆转链表只需要O(1)等等的更神奇的操作…)
散列表
Hash table,散列表,又称哈希表。一般而言使用数组来遍历,需要从头到尾依次查询,效率不算高。而如果我们能找到下标和它的卫星数据之间的关联,就可以轻易地构建查找更快的「散列表」。类比先前学过的桶排序中「构建桶」这一操作,构建散列表本质上就是构建key-value的一个结构。
注:这里的key-value并不是指java里的HashMap类的key-value!
现在想象一下手机上的电话簿,我们有数组——
String[] tele = {"萌妹+139xxxxxxxx","死宅+150xxxxxxxx","大佬+173xxxxxxxx"}
如果想要找到「大佬」的电话号码,普通的数组肯定是要遍历查找的,但如果我们构建这样的一个散列表:
- Table中,有0~25一共26个槽(slot), 每一个槽代表字母a~z。这一过程需要散列函数。
- 任意一个字母,例如d,指向所有的以d开头的一个姓名(如果储存了这个value的话)
- 由于每一个姓名绑定一串电话号码,所以我们就得到了(字母)-(姓名+电话号码)的一个key-value列表。
显然地,字母是关键字,而姓名+电话号码是卫星数据。把关键字扔进相应的槽里,这样的过程依赖散列函数。构建这样的散列表能够很容易帮助我们查询相应的数据——我们只需要得到姓名相关的第一个字母,计算这个字母所在的槽,那么我们可以在常数时间内得到我们想要的数据。
如果一个姓名绑定多串电话号码,那么就再构造一个内嵌散列表,形成(字母-姓名)和(电话号码关键字-电话号码)两个key-value。对于后面那个散列表而言,电话号码关键字会被扔到相应姓名拥有的,所有电话号码的槽里(这个关键字可能就是139,150之类的)。
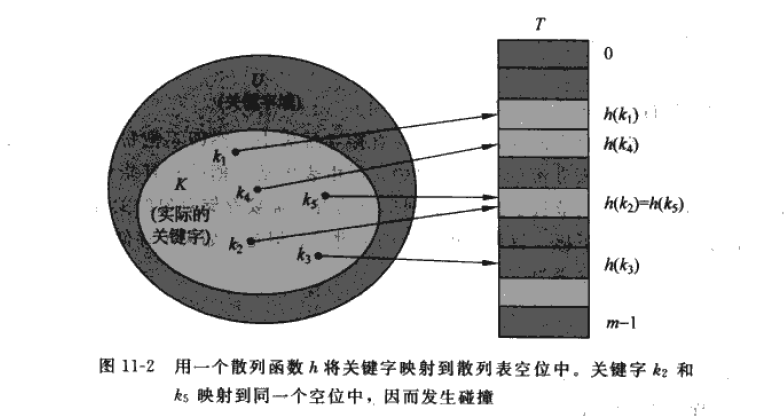
如果我们还需要储存很多的电话号码,那么难免会发生冲突(collision),多个人的关键字(第一个字母)映射到同一个槽中(比如「大佬」和「弟中弟」的「d」所指向的槽3)。对于冲突,我们需要一个合适的散列技术来解决来减少用时或者干脆减少冲突。
现在先看看造成冲突的根源——散列函数。设计一个散列函数有最常见的两种方法:除法散列和乘法散列。假设我们的关键字在0~99内选取,那么我们评定关键字储存在哪个槽,就可以用这个除法散列函数:
h(k) = k mod m
其中我们假设m取10,那么h(k)实质上是0~99中一个数的个位上的值。如果我们的关键字为02、12、22…那么这样就会造成很大的冲突。
而乘法散列函数:
h(k) = ⌊m(kA mod 1)⌋
//其中A是常数(0<A<1),kA mod 1是取kA的小数部分
则没有那么依赖m的选择了。
造成冲突之后,我们就需要散列技术来解决冲突。
-
链接法:被散列到同一个槽中的元素将被放在一个链表中,并且槽指向这个链表的表头。设有一个能存放n个元素、具有m个槽位的散列表T,那么一个链的平均存储元素数α = n/m。均匀散列的假设下,一次不成功的查找的平均时间应该为Θ(1+n/m),最坏情况仍然是O(N)。
-
开放寻址法:如果发生了冲突,则加一个常数i,然后再次调用散列函数,直到相应的位置不再发生冲突为止。这种情形显然会保证α = n/m <= 1。与完全散列不同的是,完全散列利用二级散列创立一个表中表,而开放寻址法是多次调用散列函数以保证数据仍在一级散列表中。显然α越大,空间越挤,调用函数的次数越多,耗时也就越多。
其他的知识和证明不是很有了解的必要,就先到这里了。
题目答案
第十章
10.1-6
popMode(stack1, stack2){
for(Object x:stack2);
push(stack1,pop(stack2));
}
pushMode(stack1, stack2){
for(Object x:stack1);
push(stack2,pop(stack1));
}
每次使用pop和push方法前,先调用一次popMode或者pushMode来调整至相应的模式。如果本来就是已经是相应的模式,则不调用popMode或者pushMode,并且调用相应的pop/push,那么耗时Θ(1),反之平均耗时Θ(n/2+1)。
10.1-7
transfer(queueA, queueB){
for(Object x:queueA)//except the last element
enqueue(queueB, dequeue(queueA));
dequeue(queueA);//dequeue the last element
}
if(queue1.isEmpty)
transfer(queue2, queue1);
else
transfer(queue1, queue2);
push的话跟enqueue是一样的,pop的话用另一个队列来储存上一个队列,直到最后一个值,并且放出最后一个值。
10-2
可以去了解一下二项堆(Binomial Heap),用链表来实现的一种可合并堆。可合并堆的概念在后面的「斐波那契堆」中会提到,这里篇幅太长就不写了。
第十一章
11.2-1
这是一个典型的数学问题。利用随机变量指示器描述两个不同关键字被散列到同一个槽的概率,然后求和得到结果,(n*(n-1))/(2m)。
这一章数学题很多……没什么研究的必要。